
전기 : 교류 표현 방법 (순시값, 평균값, 실효값)
순시값, 평균값, 실효값의 의미
순시값, 평균값, 실효값의 공식
순시값
순시값(RMS)은 교류 전압 또는 전류의 효과적인 값을 나타냅니다. 이는 교류 전원에서 발생하는 전압이나 전류의 크기를 DC(직류) 값으로 나타내는데 사용됩니다. RMS는 Root Mean Square의 약자로, 제곱된 값의 평균의 제곱근으로 계산됩니다.
예를 들어, 교류 전압이나 전류의 순간적인 크기는 시간에 따라 변화합니다. 이러한 교류 신호의 크기를 측정하고 평균 값을 계산하려면 순간적인 크기의 제곱을 취한 후 평균을 내야 합니다. 이 때, RMS 값을 사용하면 교류 신호의 효과적인 크기를 얻을 수 있습니다.
순시값은 다음과 같은 공식으로 계산됩니다:
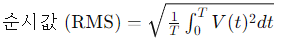
이 공식에서 T는 한 주기 동안의 시간을 나타내며, V(t)는 교류 전압의 순간적인 크기를 나타냅니다. 적분 기호
∫는 함수 V(t)2제곱의 면적을 구하는 것으로, 전압이 시간에 따라 변하는 영역을 나타냅니다. 이 면적을 한 주기 동안의 시간으로 나누고 그것의 제곱근을 취하여 RMS 값을 구합니다.
이렇게 구한 RMS 값은 교류 전압 또는 전류의 효과적인 크기를 나타내며, 이를 통해 교류 전원에서의 전력과 관련된 계산을 할 수 있습니다. RMS 값은 교류 신호의 크기를 직류 값으로 변환하는 데 사용되며, 이는 교류 전원에서의 전압이나 전류의 실제 효과를 정확하게 파악하는 데 도움이 됩니다.
평균값
평균값은 교류 전압 또는 전류의 주기 동안의 평균 값을 나타냅니다. 이는 주기 동안의 전압 또는 전류의 평균을 계산하여 얻을 수 있습니다.
교류 전원에서의 전압이나 전류는 주기적으로 변화합니다. 이러한 변화는 일반적으로 사인파 형태로 나타나며, 양의 값을 가지는 부분과 음의 값을 가지는 부분이 번갈아 나타납니다. 이에 따라 전압이나 전류의 평균값은 보통 0이 됩니다.
평균값은 다음과 같은 공식으로 계산됩니다:

이 공식에서 T는 한 주기 동안의 시간을 나타내며, V(t)는 교류 전압의 순간적인 크기를 나타냅니다. 적분 기호 ∫는 함수 V(t)의 면적을 구하는 것으로, 전압이 시간에 따라 변하는 영역을 나타냅니다. 이 면적을 한 주기 동안의 시간으로 나누어 평균 값을 계산합니다.
하지만 주기 동안의 전압 또는 전류가 양의 값과 음의 값으로 번갈아 나타나기 때문에 이 값을 그대로 사용하는 것은 일반적으로 의미가 없습니다. 따라서 보통 교류 전압이나 전류의 평균값은 0이 됩니다. 그러나 평균값은 교류 신호의 형태와 특성을 이해하고 분석하는 데 도움을 줄 수 있습니다.
순시값
순시값(RMS)은 교류(AC) 전압 또는 전류의 효과적인 값을 나타내는 중요한 개념입니다. 순시값은 교류 신호의 크기를 나타내는 데 사용되며, 이를 통해 교류 전원에서의 전력과 관련된 계산을 할 수 있습니다. 이 값을 사용하면 교류 전압이나 전류의 크기를 DC(직류) 값으로 나타낼 수 있어서 계산이나 분석이 용이해집니다.
순시값은 Root Mean Square의 약자로, 제곱된 값의 평균의 제곱근으로 계산됩니다.
아래는 순시값을 나타내는 공식입니다:

이 공식에서 T는 한 주기 동안의 시간을 나타내며, V(t)는 교류 전압의 순간적인 크기를 나타냅니다. 적분 기호
∫는 함수 V(t) 2제곱의 면적을 구하는 것으로, 전압이 시간에 따라 변하는 영역을 나타냅니다. 이 면적을 한 주기 동안의 시간으로 나누고 그것의 제곱근을 취하여 RMS 값을 구합니다.
이렇게 구한 RMS 값은 교류 전압 또는 전류의 효과적인 크기를 나타내며, 이를 통해 교류 전원에서의 전력을 정확하게 계산할 수 있습니다. RMS 값은 교류 신호의 크기를 직류 값으로 변환하는 데 사용되며, 이는 교류 전원에서의 전압이나 전류의 실제 효과를 정확하게 파악하는 데 도움이 됩니다.
'전기' 카테고리의 다른 글
| 순시값의 벡터 표현 (0) | 2024.04.21 |
|---|---|
| 파형률 및 파고율 (정의 및 계산식 , 관련문제) (0) | 2024.04.20 |
| 교류의 특성 (주기와 주파수) (0) | 2024.04.12 |
| 주기와 전기각 (의미와 공식) (0) | 2024.04.11 |
| 정현파 교류의 발생 원리 (0) | 2024.04.11 |



